Given the large size of this tip, a table of contents is provided to make faster navigation:

• How Inter-Map Transportation Works
• Defining Map Transport Relationships in the Rules.txt
  • An example from the sci-fi game
  • Understanding the Slots
  • Building Relationships from Scratch
• Assigning Map Transport Relationships to Units
• Using Events.txt to Assign Map Transport Relationships
• Scenario Solutions
  • World War II Theaters
• Credits

Before we get into how to create and use Map Transport Relationships let's discuss how units move from map to map and where they will appear on the target map. There are three methods of inter-map movement: transportation sites, starports, and native ability.

• Transportation sites works like elevators between the maps. Imagine the maps stacked one atop the other like a four-story building. What floors the elevator stops on are defined by the Map Transport Relationships. Units moving between the maps appear at the coordinates on the map transported to as the map transported from. So a unit moving from map zero coordinates 30,25 will appear at 30,25 on any other map he transports to.
  
  
• Starports allow one unit per turn to transport from one city to any other city on any map that also has a starport. In other words, it works just like an airport only it can move units between maps.
  
  
• Native transport ability uses the same principle of inter-map movement as teleportation sites only no site is required. A good example of native transport ability is the submarine, it can move between the ocean surface and ocean depths under its own power.

If upon first look at the Map Transport Relationships section of Test of Time's (hereafter referred to as ToT) Rules.txt file it appears to make no logical scene whatsoever, you are not alone. Even the most experienced scenario designers that I have spoken to felt this way. Fortunately for all of us it is not nearly as complicated as it first appears. Let us breakdown the meaning of the numbers in the rules.txt lines and it will quickly become crystal clear.

An example from the sci-fi game

We will start with the Map Transport Relationships section from ToT's sci-fi game (rules.txt):

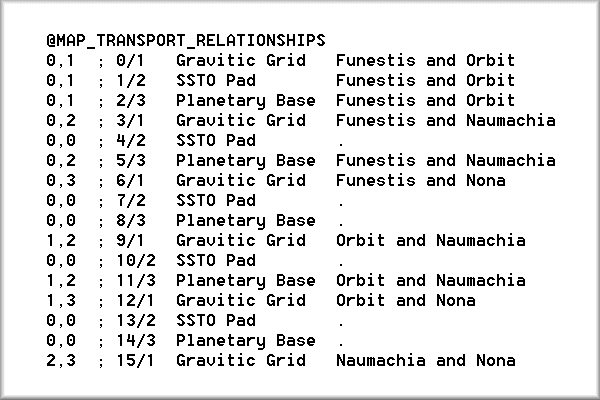
The first pair of numbers defines the map connection, map 0 to map 1, in this case.

The semi-colon defines a remark. Everything that follows the semi-colon has no effect on the processing of the rules.txt file.

The third number is the slot number for lines 0-15. This is just for reference. It is not required but it is a good idea.

The fourth number is the artwork number. Again, just for reference.

Gravitic Grid is the name of the transport site and Funestis and Orbit are the names of maps zero and one.

Understanding the Slots

The rules.txt contains sixteen slots for Map Transport Relationships, numbered zero to sixteen. No more then sixteen may be defined. There may be fewer then sixteen, but according to Microprose all sixteen slots must be filled. If you don't wish to use a given slot fill it with a null relationship such as:

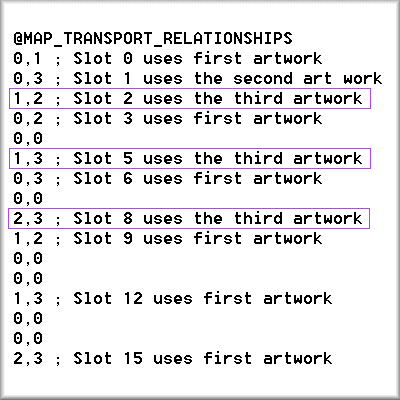
The artwork is determined by the slot number: slot 0 uses the first transport site art, slot 1 uses the second, slot 2 uses the third, slot 3 reuses the first art, slot 4 reuses the second, and so on up to 15. The three pieces of artwork are located in the cities.bmp file, the three rightmost images on the bottom row. Below is the art from the sci-fi game:

Building Relationships from Scratch

Clear as Mud? Let's do an example. If I wanted only one transport site that could transport to any map in my scenario then I would need to define six transport relationships: 0,1; 0,2; 0,3; 1,2; 1,3; 2,3. These six cover all possible map combinations. Next, I would need to assign all six relationships to one piece of art. To do this I need to define the relationships in slots 0, 3, 6, 9, 12, and 15. The others slots would need to contain filler relationships. This is how it would look:

Now let's add a map transport relationship that connects map 0 to map 3 using the second artwork.

Finally, lets add a third transport site that links maps 1, 2, and 3. Since all transport is two ways we will need only three map transport relationships (1, 2; 1,3; and 2,3) to accomplish our goal.

Now that we have setup the relationships we need to enable our units to use and build these sites and assign native transport ability where appropriate. The relationships are assigned in the @UNITS_ADVANCED section of the Rules.txt file.

Column D determines which sites a settler-type (role=5) unit may build.

Column E determines which Map Transport Relationships a unit may use.

Column F determines which Map Transport Relationships a unit has the native ability to use.

Each column consists of sixteen binary (ones or zeros) numbers for each unit. Each of these binary flags indicates whether or not a unit can use the corresponding Map Transport Relationship, a one indicating it can use it, zero indicating it can not use it. The binary flags correspond to the Map Transport Relationship in reverse programmer notation, which means that the first flag corresponds to the last relationship, slot 15, and the last flag to the first relationship, slot 0. The diagram below referring to Column E illustrates this concept.

If we want are unit to be able reach any map using our first transport site and not be able to use any of the other sites we would need to enable him to use the relationships highlighted below.

To accomplish this we would define Column E under @UNITS_ADVANCED as:

Native Transport Ability (Column F) works on the same principal as the use transport site with each binary flag referring to a Map Transport Relationship. The advantage of native transport is that no site is required to accomplish the inter-map movement.

The Build Transport Site Ability (Column D) uses the same flags as the others, of course. It is important too note that this ability is usable only by settler type units (Role=5).

Let's tackle the more advanced usage of the Map Transport Relationships, enabling units to access maps during the progression of the scenario. To do this we will need to setup events in the events.txt file that make use of the Transport action word. If you are unfamiliar with the events.txt file and the scenario macro language I strongly recommend reading the macro.txt file included on the ToT CD-ROM.

Let's say that we are making a War of the Worlds scenario, the Martians' second invasion and we define three maps:

Map 0 is the Earth's surface

Map 1 is the Earth's caverns and sewers

Map 2 is Mars

and our

@MAP_TRANSPORT_RELATIONSHIPS

0, 1 ; Slot 0, Cave Entrance, the transport site between earth's surface and caverns

0, 2 ; Slot 1, Martian Landing Pad, the transport site between Mars and Earth

1, 2 ; Slot 2, Underground Missile Silo

0, 0 ; Slot 3 Unused

…

0, 0 ; Slot 15 Unused

Our Martian units start the game with the ability to use the landing pad and our human units may use the cave entrances, but neither may use the other.

During our scenario we want the humans to learn how to use the Martian transport sites when they capture a Martian Commander. To do this we will setup a UnitKilled trigger and a Transport action.

The Human discovery of High Efficiency Rocket Fuel would allow Human Missiles to hit targets on Mars from their underground bases.

The imagination and heap size are the only limits to the possibilities with events, so create and enjoy.

Understanding how to define Map Transport Relationships is only the first half of what the scenario designer needs to know. How to make map transportation work within the theme of the scenario is the other half. Making the rules and limitations of the civ engine mesh seamlessly with the theme and playability of the scenario is the true art of 'scenariocraft'.

World War II Theatres

Let us suppose that we are making a two theater WWII scenario with map zero being the European Theater and map one the Pacific Theater. What type of map transport will best suit our scenario?

Native transport ability could be ruled out from the start in this example. German Panzer Divisions that could teleport from the Ural Mountains to the outskirts of Seattle would detract from the historical accuracy of the scenario. One could argue that the British and American fleets should have the native transport ability, but consider the abuses this could create. Disembarking from Portsmouth, England a transport loaded with Marines would probably appear in the Pacific within striking distance of Tokyo.

Predefined transport sites could limit the scope of the abuse but the layouts of the theaters of war do not lend themselves to their use. A connection between Gibraltar and India for British only use would make sense but how could we deal with America being on the West side of one map and the East side of another?

That leaves the only other possibility of using starports. We could start by renaming starport to inter-theater port facility (or some such name) and making it impossible to build. By locating these inter-theater connection points in strategic cites such as Suez, Gibraltar, London, New York, San Diego, Seattle, Hong Kong, and Tokyo we can simulate the ability to strategically re-deploy troops from one theater to another. Thus, the Germans would not be able to send troops to Japan until they have taken the Suez or Gibraltar. Likewise the Allies would have realistic limits on how many units they could move from theater to theater, perhaps two or three per turn.

Written by William Keenan.

Contributors include Techumseh, John Possidente, and Cam Hills.